|
|
tiếp theo...
Thậm chí một số còn cho rằng khoa học ngày nay đã tiến gần đến cái ngưỡng đó. Thời gian sẽ trả lời nhận định này đúng hay sai.
Tuy nhiên, sự tồn tại của một cái ngưỡng là có thật, ít nhất điều này đã được chứng minh trong Toán Học và trong Khoa Học Computer: Đó là “Định Lý Bất Toàn” (Theorem of Incompleteness) của Kurt Godel và “Sự Cố Dừng” (The Halting Problem) của Alan Turing.
Cái ngưỡng đó làm cho một số người nản lòng, thậm chí cảm thấy khó chịu, vì không thể chấp nhận một cái ngưỡng ngáng trở nhận thức. Xin nói ngay rằng những người đó đã hiểu lầm: Chính cái ngưỡng đó làm cho cuộc sống của chúng ta có ý nghĩa hơn, hạnh phúc hơn, và khoa học sẽ đâm chồi nẩy lộc nhiều hơn, đơm hoa kết trái nhiều hơn!
Thật vậy, vì nhận thức có giới hạn, nó không bao giờ đạt tới đích cuối cùng, vì thế khát vọng khám phá sẽ được nuôi dưỡng mãi mãi, niềm vui khám phá sẽ không bao giờ cạn, trí tưởng tượng của con người sẽ tha hồ bay bổng, … điều này làm nên một trong những ý nghĩa căn bản của cuộc sống.
Immanuel Kant vĩ đại từng nói: “Mỗi câu trả lời lại đặt ra một câu hỏi mới”. Bạn nghĩ sao nếu chúng ta tìm ra một câu trả lời cho mọi thứ để rồi không còn gì đáng hỏi nữa? Cuộc sống khi đó sẽ ra sao? Nhưng chính vì không bao giờ có một câu trả lời cuối cùng nên con người tha hồ tưởng tượng để tìm câu trả lời cho những gì mình chưa biết. Nhà toán học kiêm triết học nổi tiếng Bertrand Russell đã an ủi những người lo xa: “Khoa học có thể tạo ra giới hạn đối với sự hiểu biết, nhưng không tạo ra giới hạn đối với trí tưởng tượng”2.
Nói cách khác, Bà Mẹ Tự Nhiên (The Mother Nature) không bao giờ mở cánh cửa bí mật cuối cùng cho chúng ta, mà luôn để dành những bí mật tiếp theo cho chúng ta khám phá, nhằm nuôi dưỡng chúng ta không chỉ phần xác, mà cả phần hồn!
Bí mật của Tự Nhiên giống như “Chiếc Hộp Trung Hoa” (Chinese Box) hoặc những con búp-bê Matryoshka của Nga – mỗi lần mở ra lại thấy một chiếc hộp bên trong (một con búp-bê bên trong). Mỗi chúng ta đều giống như một đứa trẻ tò mò, trông thấy chiếc hộp bên trong lại muốn mở ra xem, và lại thấy một chiếc hộp bên trong nữa. Albert Einstein chính là một đứa trẻ điển hình như thế, ông nói: “Cái đẹp nhất mà chúng ta có thể chiêm nghiệm chính là sự BÍ ẨN. Đó là ngọn nguồn của nghệ thuật và khoa học chân chính” 3
Vậy thay vì chống đối nguyên lý giới hạn của nhận thức, chúng ta nên cảm ơn nó, vì nhờ nó chúng ta luôn sống với những khát vọng lãng mạn!
Nhưng cần phải tỉnh táo, vì nếu tham vọng nhận thức trở thành vô chừng vô độ, bất chấp giới hạn thì đó lại là một vấn đề hoàn toàn khác!
2] Khi tham vọng trở nên vô chừng vô độ:
Khi đó, nhận thức có nguy cơ rơi vào không tưởng, lầm đường lạc lối, thay vì tiến lên, nhận thức trở thành một cái vòng luẩn quẩn, hoặc thậm chí thụt lùi.
Lịch sử đã từng chứng kiến phản ứng của những người nhìn xa trông rộng trước những kiểu tham vọng vô chừng vô độ như thế. Một trong những trường hợp đáng để cho chúng ta phải suy ngẫm nghiêm túc lại là Albert Einstein. Bạn nghĩ sao khi một người như Einstein – một người có khát vọng hiểu biết cháy bỏng hơn ai hết, một đứa trẻ từng say đắm Hình Học Euclid như một kỳ quan, một nhà vật lý cần toán học như chúng ta cần không khí và nước – đã có lúc phải thốt lên:
“Tôi không tin vào Toán Học”4!
Thoạt nghe, có vẻ như đó là một chuyện bịa đặt, nhưng than ôi, đó lại là một sự thật! Xin bạn hãy bình tâm tìm hiểu sự thật này, và tôi tin rằng bạn sẽ hết ngạc nhiên nếu biết rõ rằng ấy là lúc Einstein phản ứng với những thứ toán học sáo rỗng, hình thức chủ nghĩa, toán học siêu hình (meta-mathematics), toán học tách rời thực tiễn, toán học thuần tuý suy diễn logic mà không đếm xỉa đến ý nghĩa thực tế.
Bạn sẽ dễ dàng thông cảm với Einstein nếu biết rõ rằng thứ toán học siêu hình đó đã ra đời từ một tham vọng vô chừng vô độ và không tưởng của một số nhà toán học cùng thời với ông. Những người này tin rằng tồn tại những chân lý logic hình thức tuyệt đối, độc lập với thế giới hiện thực xung quanh, và tin rằng với những phương pháp nghiên cứu đúng đắn, trước sau họ cũng sẽ tìm ra những chân lý tuyệt đối đó.
Nhưng Einstein, với trực giác siêu việt, ngay từ đầu đã không tin họ, không tin vào tham vọng ngông cuồng của họ, không tin vào hệ thống toán học thuần lý bất chấp thực tiễn của họ, và lịch sử đã đứng về phía Einstein!
Chẳng riêng Einstein, một vĩ nhân khác mà tài năng chẳng kém gì Einstein là Henri Poincaré, người được coi là Mozart của Toán Học, cũng chống đối quyết liệt thứ toán học sính hình thức đó.
Nhưng than ôi! Sức ỳ của bộ não cũng “vĩ đại” chẳng kém gì sức sáng tạo của nó: Bất chấp những người như Einstein và Poincaré, tư tưởng sính hình thức trong giới toán học, và đặc biệt trong giới giảng dạy toán học, vẫn cứ tiếp tục sống dai dẳng cho đến tận hôm nay.
Nếu đọc giả để ý quan sát, sẽ chẳng mấy khó khăn để nhận thấy bóng dáng những loại toán học này trong hệ thống giáo dục hiện nay. Đó là hậu quả tàn dư của thứ toán học hình thức mà Einstein và Poincaré chán ghét. Đó là lý do để nhiều học giả trên thế giới ngày nay phải lên tiếng cảnh báo: Hãy tỉnh táo để nhận thức nguyên lý giới hạn của nhận thức!
Trong bối cảnh đó, tích “Thầy Bói Xem Voi” tất yếu mang ý nghĩa thời sự và được làm sống lại một cách sinh động dưới nhiều hình thức, điển hình là những “mô hình bất khả” (Impossible Models), hay những “cấu trúc phi lý” (Inconsistent Structures).
3] Mô Hình Bất Khả:
Điển hình của những mô hình này là Tam Giác Penrose hoặc Bậc Thang Penrose của Sir Roger Penrose, một trong những nhà vật-lý-toán-học lớn nhất ngày nay. Ông có những đóng góp vô cùng đa dạng trong vật lý và toán học, đoạt rất nhiều giải thưởng danh giá bậc nhất về vật lý và toán. Cùng với Stephen Hawking, ông được coi là một trong những tác giả của Lý thuyết về hốc đen, như Wikipedia nhận định: “Công trình sâu sắc của ông về tính Tương Đối Tổng Quát đóng vai trò chủ yếu trong nhận thức của chúng ta về các hốc đen”. Nhưng khác với Stephen Hawking, ông không mấy tin tưởng vào khả năng “Hiểu được ý Chúa” của Einstein trước đây và của Hawking hiện nay. Bản thân những “mô hình bất khả” của ông đã nói lên điều đó.

Những mô hình bất khả của Penrose
Ngắm kỹ hai mô hình trên, dễ nhận thấy chúng chỉ “khả dĩ” (possible) hoặc “hợp lý” (consistent) trong từng cục bộ (local part), nhưng “bất khả” (impossible) hoặc “phi lý” (inconsistent) trên tổng thể (the whole), đúng như triết lý của “Thầy Bói Xem Voi”: Mỗi anh đúng một phần, Nhưng đều sai tất cả!
Tuy nhiên sẽ là bất công nếu gán cho các nhà khoa học công lao sáng tạo ra những “mô hình bất khả”. Chính các hoạ sĩ mới là những người đi tiên phong trong lĩnh vực này. Hãy ngắm bức tranh sau đây:
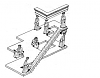
“Cầu thang bất khả” (Impossible Staircase) cuả Reutersvard
Đó là cấu trúc “Cầu thang bất khả” (Impossible Staircase) cuả hoạ sĩ Thụy Điển Oscar Reutersvard (1915-2002) được vẽ từ nửa đầu thế kỷ 20! Với hàng trăm mô hình tương tự, Reutersvard được coi là cha đẻ của ngành “hội hoạ ảo ảnh” (Illusionary Art), và chính hội hoạ đó đã tạo cảm hứng cho Penrose sáng tạo ra những mô hình của mình.
Tuy nhiên phải thừa nhận rằng, từ khi những nhà khoa học lớn như Penrose sử dụng các mô hình bất khả để nói lên nguyên lý bất khả trong việc nhận thức CÁI TOÀN BỘ, thì nguyên lý này mới được nhìn nhận một cách thực sự nghiêm túc, không chỉ dưới hình thức văn chương, nghệ thuật, hoặc triết học, mà ngay cả trong lĩnh vực khoa học và công nghệ. Điều này rất có lợi cho cuộc sống, vì nó hướng khoa học vào những công trình thực dụng hơn, thiết thực hơn. Sự chuyển hướng này bộc lộ rất rõ trong những Giải Nobel khoa học từ cuối thế kỷ 20 tới nay (trước đây thường dành cho những đề tài thuần tuý lý thuyết).
Tóm lại, đã có một sự bừng tỉnh về nhận thức đối với triết lý “Thầy Bói Xem Voi”. Để cảm nhận được điều đó, bạn chỉ cần ngồi vào computer rồi gõ “impossible models”, hoặc “artistic illusions”, “inconsistent art”, v.v. bạn sẽ có hàng trăm, hàng nghìn mô hình “bất khả” kỳ lạ khác nhau, trong đó rất nhiều mô hình vừa được công bố chỉ vài ngày trước khi bài báo này đến tay bạn. Điều đó nói lên rằng chủ đề này nóng hổi đến chừng nào.
Tuy nhiên, nếu bạn thật sự muốn biết các nhà khoa học và giáo dục ngày nay nghĩ gì về triết lý “Thầy Bói Xem Voi”, xin bạn hãy đọc ngay một cuốn “best-seller” của năm 1998: “What is Mathematics, Really?” (Thực ra Toán Học là gì?) cuả Reuben Hersh, một nhà toán học rất nổi tiếng ở Mỹ, trong đó tác giả đã dẫn nguyên văn truyện Sáu anh mù ở xứ Indostan để nói về một “giấc mơ vĩ đại” của các nhà toán học trong thế kỷ 20 – Giấc mơ tìm thấy “Con Voi Toán Học”!

4] Thay lời kết:
Câu chuyện về giấc mơ tìm kiếm Con Voi Toán Học là một trong những chương có ý nghĩa nhất và quan trọng nhất trong lịch sử toán học – quan trọng đến nỗi nếu không biết gì về nó thì không những sẽ vô cùng thiệt thòi vì đã bỏ qua một trong những chương hay nhất, hấp dẫn nhất của lịch sử khoa học, mà còn có nguy cơ bị thiếu hụt một bài học vô giá về khoa học nhận thức và khoa học giáo dục.
Sự thiếu hụt ấy sẽ dẫn tới hậu quả không hiểu rõ bản chất của toán học, và do đó sẽ áp dụng một phương pháp sai lầm trong giảng dạy toán học. Đó chính là điều Reuben Hersh muốn nói, và cũng là điều mà loạt bài viết về chủ đề “Thầy Bói Xem Voi” muốn nói.
Quả thật là đang tồn tại tình trạng hiểu sai bản chất toán học, và đó là lý do căn bản dẫn tới tình trạng “dạy giả” và “học giả” tràn lan: Chưa bao giờ tình trạng học sinh không hiểu Toán, đối phó với Toán, chán Toán, sợ Toán, … ngày càng trở nên phổ biến như hiện nay.
Công bằng mà nói, tình trạng này không chỉ xẩy ra tại Việt Nam, mà đã từng xẩy ra ở ngay tại một số quốc gia phát triển, khi những quốc gia này áp dụng một phương pháp dạy Toán mà họ tưởng là “mới”. Nhưng lịch sử giáo dục đã chứng minh rằng những phương pháp gọi là “mới” đó thực chất chỉ là sản phẩm của một tham vọng không tưởng – tham vọng tìm kiếm Con Voi Toán Học. Chính vì không tưởng nên nó đã đổ vỡ tan tành!
Tại sao một tham vọng đã đổ vỡ mà vẫn còn ảnh hưởng đến nền giáo dục hôm nay? Đó là một ẩn số cần được trả lời, và sẽ được trả lời trong bài kỳ sau: “Giấc mơ tìm kiếm Con Voi Toán Học”, hoặc gọi theo cách của các nhà triết học khoa học tây phương hiện nay, “Giấc mơ tìm kiếm Chiếc Chén Thánh Toán Học”.
Sydney ngày 01 tháng 01 năm 2009
Phạm Việt Hưng
[1] Indostan là một tên gọi cổ được sử dụng nhiều trong các thế kỷ 17, 18, 19, để gọi một vùng địa lý mà ngày nay ta gọi là Nam Á, bao gồm Ấn Độ, Pakistan, Bangladesh, Sri Lanka, Maldives, Bhutan và Nepal (những quốc gia nói chung có khí hậu nóng và chịu nhiều ảnh hưởng của nền văn minh Ấn Độ).
[2] Nguyên văn: “Science may set limits to knowledge, but should not set limits to imagination”
[3] Xem “Phương trình của Chúa” của Phạm Việt Hưng trên Khoa Học & Tổ Quốc, số 3+4/2005
[4] Nguyên văn: “I don’t believe in Mathematics”. Xem “Impossibility” của John Barrow.
© http://vietsciences.free.frr và http://vietsciences.org Phạm Việt Hưng
|
|










 Trả lời với trích dẫn
Trả lời với trích dẫn